TSF : A Space Odyssey Uzay Kozmoloji Konular─▒
Forum kurallar─▒
Sevgili ├£yeler Forum Kurallar─▒nda Tart─▒┼¤─▒lmas─▒ Uygun Olmad─▒─¤─▒ Belirtilen Konular Hakk─▒nda Bu B├Čl├╝mde Payla┼¤─▒m ve Fikir Bildirimi Yapmay─▒n─▒z. ─░nan├¦lar, Politika, Fanatizm, Irk├¦─▒l─▒k Vb. ─░├¦eriklerde Konular A├¦may─▒n─▒z. Ayr─▒ca Ki┼¤isel Mahremiyet ve Ailesel Durumlar─▒n─▒z─▒ ─░├¦eren Konular─▒ Burada Payla┼¤may─▒n─▒z. Birbirinize Sayg─▒l─▒ Olunuz L├╝tfen.
Sevgili ├£yeler Forum Kurallar─▒nda Tart─▒┼¤─▒lmas─▒ Uygun Olmad─▒─¤─▒ Belirtilen Konular Hakk─▒nda Bu B├Čl├╝mde Payla┼¤─▒m ve Fikir Bildirimi Yapmay─▒n─▒z. ─░nan├¦lar, Politika, Fanatizm, Irk├¦─▒l─▒k Vb. ─░├¦eriklerde Konular A├¦may─▒n─▒z. Ayr─▒ca Ki┼¤isel Mahremiyet ve Ailesel Durumlar─▒n─▒z─▒ ─░├¦eren Konular─▒ Burada Payla┼¤may─▒n─▒z. Birbirinize Sayg─▒l─▒ Olunuz L├╝tfen.
Re: TSF : A Space Odyssey Uzay Kozmoloji Konular─▒
Akl─▒n fikrin yemekte. Sen denklemi t├╝ret sana bir ├ćokoprens, bir Halley, bir de Ferroro Rocher..
"Evrende en b├╝y├╝k ziyan, sorgulama yetene─¤ini yitirmi┼¤ bir beyindir." - A. Einstein
-

asymptote - Mesajlar: 12140
- Kay─▒t: 11 Ara 2010, 14:28
Re: TSF : A Space Odyssey Uzay Kozmoloji Konular─▒
Baran yazd─▒:Turetemeyenede benden Ferroro Rocher
Adresi ├¢M at─▒yorum karde┼¤im
Instagram:
watchtron
anatoliastraps
watchtron
anatoliastraps
-

mlm - Mesajlar: 23962
- Ya┼¤: 44
- Kay─▒t: 03 A─¤u 2010, 02:59
- Konum: Ankara
Re: TSF : A Space Odyssey Uzay Kozmoloji Konular─▒
asymptote yazd─▒:Miriel yazd─▒:En son F=m.a da kalm─▒┼¤t─▒m.
Oradan devam edeceksin i┼¤te.. ─░pucu vereyim:
Newton mekani─¤ine g├Čre bir k├╝tlenin sahip olabilece─¤i iki t├╝r enerji vard─▒r ve bu enerjilerin toplam─▒ sabittir, zamanla de─¤i┼¤mez (siz bu sabiti -kc^2 kabul edin).
Denklemde yer alan a ├Čl├¦ek fakt├Čr├╝d├╝r, keyfi bir uzunluktur ve Hubble parametresinde yer al─▒r.
H=(da/dt)/a, V=H*D
V: velocity, H: Hubble parameter, D: Distance
Ne yaz─▒k ki ├¦ok yabanc─▒ oldu─¤um konular ...
─░kinci b├Čl├╝mde bu tarz form├╝l ├¦─▒kar─▒mlar─▒ yapmay─▒ gerektiren sorular─▒ severek yap─▒yordum. (Klasik fizik ve g├Črelilik..). Ama e┼¤it a─¤─▒rl─▒k├¦─▒ olarak art─▒k bu konulara ├¦ok uza─¤─▒m.
Ama ispat─▒ merakla bekliyorum.

NOBLESSE OBLIGE!
-

Miriel - Mesajlar: 3123
- Kay─▒t: 03 A─¤u 2011, 20:08
Re: TSF : A Space Odyssey Uzay Kozmoloji Konular─▒
Y├╝ksek├Č─¤renime ba┼¤l─▒yorsun, yeni bir├¦ok ┼¤ey ├Č─¤reneceksin, heyecan─▒n─▒ anl─▒yorum. Fakat yeteneklerini ve ilgi alanlar─▒n─▒ okuyaca─¤─▒n b├Čl├╝mle s─▒n─▒rland─▒rma. ─░kinci b├Čl├╝mde severek ├¦├Čzd├╝─¤├╝n konularla ilgilenmeye yine devam edebilirsin. Okul ├Čnceli─¤in olsun elbette, ama duyargalar─▒n─▒ farkl─▒ disiplinlere de a├¦..
"Evrende en b├╝y├╝k ziyan, sorgulama yetene─¤ini yitirmi┼¤ bir beyindir." - A. Einstein
-

asymptote - Mesajlar: 12140
- Kay─▒t: 11 Ara 2010, 14:28
Re: Ynt: TSF : A Space Odyssey Uzay Kozmoloji Konular─▒
Benim duyargalarim basta yemek olmak uzere otomobiller guzel kizlar ,geleneksel tras , saatler ve meslegim mimarliga acik sadece.Bu konular beni cezbetmiyor maksat sizlerle ayni cati altinda bulusmak.Bakin artik uzaylilara rakida icirmiyorum  mlm adini listeye yazdim abi cok basvuru oldu
mlm adini listeye yazdim abi cok basvuru oldu 
-

Baran - Mesajlar: 13237
- Ya┼¤: 40
- Kay─▒t: 02 ┼×ub 2011, 23:10
- Konum: Istanbul
Re: TSF : A Space Odyssey Uzay Kozmoloji Konular─▒
Sen duyargalar─▒n─▒ sonuna kadar a├¦m─▒┼¤s─▒n zaten..  Senin ve di─¤er arkada┼¤lar─▒n duyargalar─▒n─▒ bu konuya da biraz a├¦al─▒m istiyorum. ├ć├╝nk├╝ menfaatinize olaca─¤─▒n─▒ biliyorum. Bu konular az bir ├¦abayla ├¦ok keyif alaca─¤─▒n─▒z konular. Dolay─▒s─▒yla amat├Čr d├╝zeyde f(orce)/p(leasure) oran─▒ ├¦ok ├¦ok iyi. Hem sadece d├╝nyan─▒n de─¤il, ayn─▒ zamanda evrenin de en ├Čnemli konusu kozmoloji..
Senin ve di─¤er arkada┼¤lar─▒n duyargalar─▒n─▒ bu konuya da biraz a├¦al─▒m istiyorum. ├ć├╝nk├╝ menfaatinize olaca─¤─▒n─▒ biliyorum. Bu konular az bir ├¦abayla ├¦ok keyif alaca─¤─▒n─▒z konular. Dolay─▒s─▒yla amat├Čr d├╝zeyde f(orce)/p(leasure) oran─▒ ├¦ok ├¦ok iyi. Hem sadece d├╝nyan─▒n de─¤il, ayn─▒ zamanda evrenin de en ├Čnemli konusu kozmoloji..
Hadi beyler, kazanan siz olabilirsiniz..

Hadi beyler, kazanan siz olabilirsiniz..

"Evrende en b├╝y├╝k ziyan, sorgulama yetene─¤ini yitirmi┼¤ bir beyindir." - A. Einstein
-

asymptote - Mesajlar: 12140
- Kay─▒t: 11 Ara 2010, 14:28
Re: TSF : A Space Odyssey Uzay Kozmoloji Konular─▒
├¢d├╝ll├╝ soru i├¦in tan─▒nan s├╝re ├¦oktan doldu. Madem bir yan─▒t gelmedi biz de cevab─▒ yay─▒nlayal─▒m:
Miriel'i k─▒rmayal─▒m ve F=ma'dan ba┼¤layal─▒m. Bildi─¤iniz gibi enerji kuvvetin bir yol boyunca etkimesidir. Kuvvetin kayna─¤─▒ da k├╝tle ├¦ekimi ya da momentum de─¤i┼¤imi olabilir. Momentum de─¤i┼¤imiyle ili┼¤kili kuvvetten kaynaklanan enerji kinetik enerjidir.

K├╝tle ├¦ekimiyle ili┼¤kili kuvvetten kaynaklanan enerji ise potansiyel enerjidir.

─░zotropik ve homojen kabul etti─¤imiz evrende bir k├╝resel uzay ele alal─▒m. Bu k├╝resel uzay i├¦inde homojen ve izotropik da─¤─▒lm─▒┼¤ galaksiler olsun. Y├╝zeyde V h─▒z─▒yla hareket etmekte olan rijit bir objenin (├Črne─¤imizde galaksinin) kinetik ve potansiyel enerjilerinin toplam─▒ sabittir ve zaman i├¦inde de─¤i┼¤mez (enerjinin korunumu prensibi..) De─¤i┼¤meyen bu sabite biz -k diyelim.

Yukar─▒daki denklemde e┼¤itli─¤in her iki taraf─▒n─▒ 2 ile ├¦arpar ve k├╝tleye b├Člersek a┼¤a─¤─▒daki denklemi elde ederiz.

Burada e┼¤itli─¤in sa─¤ taraf─▒ yine -k olarak kalm─▒┼¤t─▒r, ├¦├╝nk├╝ bir sabitin ba┼¤ka bir sabit ile ├¦arp─▒m─▒ yine bir sabittir ve olu┼¤an bu yeni sabit tekrar ayn─▒ sembolle g├Čsterilebilir..
Di─¤er taraftan Hubble Yasas─▒'ndan biliyoruz ki evrendeki bir objenin h─▒z─▒ mesafesiyle do─¤ru orant─▒l─▒d─▒r. Buradaki orant─▒ sabiti Hubble parametresi ad─▒n─▒ al─▒r ve ├Čl├¦ek fakt├Čr├╝n├╝n (a) zamana g├Čre de─¤i┼¤iminin kendisiyle oran─▒d─▒r. A┼¤a─¤─▒daki e┼¤itlikte yer alan x a─¤lara b├Čl├╝nm├╝┼¤ uzayda iki nokta aras─▒ndaki grid say─▒s─▒d─▒r (say─▒sal bir de─¤erdir..) S ise mesafe olup D ile de g├Čsterilir.

Yukar─▒daki D ve V'yi II nolu denklemde yerine yazarsak ve yo─¤unlu─¤u dahil edersek

denklem a┼¤a─¤─▒daki hali al─▒r

burada e┼¤itli─¤in sol taraf─▒ x'in karesi ile orant─▒l─▒ oldu─¤undan sa─¤ taraf da ayn─▒ ┼¤ekilde x^2 ile orant─▒l─▒ olmak durumundad─▒r. O halde e┼¤itli─¤in her iki taraf─▒ndan x^2 terimlerini kald─▒rabiliriz ve denklemi a┼¤a─¤─▒daki forma sokar─▒z

Bu denklemde k'n─▒n yan─▒na c^2 (c: ─▒┼¤─▒k h─▒z─▒) koyarsak k sabitimiz birimsiz bir say─▒sal de─¤ere d├Čn├╝┼¤├╝r.

Bu denkleme Friedman Denklemi denir. Friedman denklemi eksikleri olsa da kozmolojinin temel denklemi kabul edilir. Bu denklemdeki k sabitine ise e─¤rilik fakt├Čr├╝ (curvature factor) denir. K sabitinin pozitif, negatif ya da s─▒f─▒r olmas─▒ uzay─▒n farkl─▒ e─¤rili─¤e (forma) sahip olmas─▒ anlam─▒na gelir.
K>0 ise kapal─▒ form k├╝resel uzay, K<0 ise a├¦─▒k form hiperboloit uzay, K=0 ise a├¦─▒k form d├╝z uzay (bildi─¤imiz Euclid uzay─▒) s├Čz konusudur.
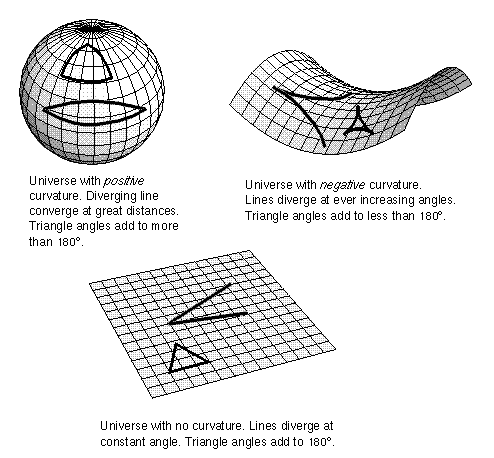
Uzay─▒n hangi formda oldu─¤unu bilmemekle beraber, Euclid uzay─▒nda oldu─¤umuzu d├╝┼¤├╝n├╝yoruz. Bu konudaki ├Čl├¦├╝mler (high precision cosmology) geli┼¤irse ileride belki bizi ┼¤a┼¤─▒rtacak bir sonu├¦la da kar┼¤─▒la┼¤abiliriz. K>0 ise (uzay kapal─▒ k├╝resel formda ise) bu ┼¤u anlama gelir:
T─▒pk─▒ bir k├╝renin y├╝zeyinde (├Črne─¤in d├╝nyam─▒zda) s├╝rekli ayn─▒ y├Čne ilerledi─¤imizde nas─▒l bir s├╝re sonra ba┼¤lad─▒─¤─▒m─▒z noktaya geri d├Čn├╝yorsak k├╝resel uzayda da ayn─▒ ┼¤ey s├Čz konusu olur. Bu sefer bir y├╝zey ├╝zerinde de─¤il de 3 boyutlu uzayda ilerlemi┼¤ oluruz, tek fark budur. Ben e─¤rilik fakt├Čr├╝n├╝n s─▒f─▒rdan b├╝y├╝k olmas─▒n─▒ daha heyecanl─▒ buluyorum (umar─▒m bir g├╝n b├Čyle oldu─¤u ortaya ├¦─▒kar..)
Friedman Denklemini elde etti─¤imize g├Čre bu denklemde yer alan, zamana g├Čre de─¤i┼¤en ba─¤─▒ml─▒ de─¤i┼¤keni (├Čl├¦ek fakt├Čr├╝n├╝) d├╝z uzay (k=0) kabul├╝yle elde etmeye ├¦al─▒┼¤al─▒m. ├¢l├¦ek fakt├Čr├╝ bize uzay─▒n zamana g├Čre nas─▒l geni┼¤ledi─¤ini (ya da darald─▒─¤─▒n─▒) g├Čsteren ve Hubble Parametresinde yer alan ├Čnemli bir de─¤i┼¤kendir. Friedman denklemi do─¤rusal olmayan bir diferansiyel denklemdir ve analitik ├¦├Čz├╝m├╝ ├¦ok kolay de─¤ildir. Bu t├╝r denklemlerin ├¦├Čz├╝m├╝nde s─▒k├¦a ba┼¤vurulan bir y├Čntem tahmini bir de─¤er ile ├¦├Čz├╝m├╝ sorgulamakt─▒r. ├¢l├¦ek fakt├Čr├╝ zamana ba─¤l─▒ bir fonksiyondur ve polinom formunda olabilece─¤i gibi ├╝stel ya da logaritmik vb. formda da olabilir. Friedman denkleminde e┼¤itli─¤in sa─¤ taraf─▒ s─▒f─▒rdan farkl─▒ bir de─¤er oldu─¤undan e┼¤itli─¤in sol taraf─▒ asla bir b├╝k├╝m noktas─▒na sahip olmamal─▒d─▒r (a de─¤i┼¤keni zamanla s├╝rekli artan ya da s├╝rekli azalan bir de─¤i┼¤ken olmal─▒d─▒r). Uzay s├╝rekli daralamayaca─¤─▒na g├Čre s├╝rekli geni┼¤lemelidir, buradan bu sonu├¦ ├¦─▒k─▒yor. O halde a zamanla artan pozitif bir de─¤erdir. a=c.t^p diyelim.

Sonucu III nolu denklemde (k=0) yerine yazarsak ├¦├Čz├╝m├╝ a┼¤a─¤─▒daki ┼¤ekilde elde etmi┼¤ oluruz.


a i├¦in elde etti─¤imiz yukar─▒daki VI numaral─▒ denklem bize uzay─▒n zamana g├Čre ne ┼¤ekilde geni┼¤ledi─¤ini g├Čsteriyor.
Rahmetli bu denklemi (III nolu denklem) Einstein'─▒n genel g├Črelilik kuram─▒ndan t├╝retmi┼¤tir, ancak bu denklem Newton mekani─¤inden de t├╝retilebiliyor. Buradaki ├¦├Čz├╝mlemedeki enerji yo─¤unlu─¤u olarak k├╝tle esas al─▒nm─▒┼¤t─▒r (mass dominated universe kabul├╝ yap─▒lm─▒┼¤t─▒r). Ancak uzay ilk zamanlarda ├¦ok daha dard─▒ ve fotonlar─▒n dalga boylar─▒ k├╝├¦├╝k dolay─▒s─▒yla frekanslar─▒ ve enerji d├╝zeyleri y├╝ksekti. Uzay─▒n bu ilk zamanlar─▒ i├¦in enerji yo─¤unlu─¤u olarak fotonlar─▒ esas alan (radiation dominated universe) bir ├¦├Čz├╝mleme de yap─▒labilir. Bu ├¦├Čz├╝mleme yap─▒l─▒rsa uzay─▒n ilk zamanlar t'nin 2/3 de─¤il de 1/2 kuvveti oran─▒nda geni┼¤ledi─¤i ortaya ├¦─▒k─▒yor. Bu ├¦├Čz├╝mlemeyi dahil etmedim, gerek de yok, olan olmu┼¤ bir kere.. ┼×imdi k├╝tle esasl─▒ ├¦├Čz├╝m yapmal─▒, biz de onu yapt─▒k zaten..
Miriel'i k─▒rmayal─▒m ve F=ma'dan ba┼¤layal─▒m. Bildi─¤iniz gibi enerji kuvvetin bir yol boyunca etkimesidir. Kuvvetin kayna─¤─▒ da k├╝tle ├¦ekimi ya da momentum de─¤i┼¤imi olabilir. Momentum de─¤i┼¤imiyle ili┼¤kili kuvvetten kaynaklanan enerji kinetik enerjidir.

K├╝tle ├¦ekimiyle ili┼¤kili kuvvetten kaynaklanan enerji ise potansiyel enerjidir.

─░zotropik ve homojen kabul etti─¤imiz evrende bir k├╝resel uzay ele alal─▒m. Bu k├╝resel uzay i├¦inde homojen ve izotropik da─¤─▒lm─▒┼¤ galaksiler olsun. Y├╝zeyde V h─▒z─▒yla hareket etmekte olan rijit bir objenin (├Črne─¤imizde galaksinin) kinetik ve potansiyel enerjilerinin toplam─▒ sabittir ve zaman i├¦inde de─¤i┼¤mez (enerjinin korunumu prensibi..) De─¤i┼¤meyen bu sabite biz -k diyelim.

Yukar─▒daki denklemde e┼¤itli─¤in her iki taraf─▒n─▒ 2 ile ├¦arpar ve k├╝tleye b├Člersek a┼¤a─¤─▒daki denklemi elde ederiz.

Burada e┼¤itli─¤in sa─¤ taraf─▒ yine -k olarak kalm─▒┼¤t─▒r, ├¦├╝nk├╝ bir sabitin ba┼¤ka bir sabit ile ├¦arp─▒m─▒ yine bir sabittir ve olu┼¤an bu yeni sabit tekrar ayn─▒ sembolle g├Čsterilebilir..
Di─¤er taraftan Hubble Yasas─▒'ndan biliyoruz ki evrendeki bir objenin h─▒z─▒ mesafesiyle do─¤ru orant─▒l─▒d─▒r. Buradaki orant─▒ sabiti Hubble parametresi ad─▒n─▒ al─▒r ve ├Čl├¦ek fakt├Čr├╝n├╝n (a) zamana g├Čre de─¤i┼¤iminin kendisiyle oran─▒d─▒r. A┼¤a─¤─▒daki e┼¤itlikte yer alan x a─¤lara b├Čl├╝nm├╝┼¤ uzayda iki nokta aras─▒ndaki grid say─▒s─▒d─▒r (say─▒sal bir de─¤erdir..) S ise mesafe olup D ile de g├Čsterilir.

Yukar─▒daki D ve V'yi II nolu denklemde yerine yazarsak ve yo─¤unlu─¤u dahil edersek

denklem a┼¤a─¤─▒daki hali al─▒r

burada e┼¤itli─¤in sol taraf─▒ x'in karesi ile orant─▒l─▒ oldu─¤undan sa─¤ taraf da ayn─▒ ┼¤ekilde x^2 ile orant─▒l─▒ olmak durumundad─▒r. O halde e┼¤itli─¤in her iki taraf─▒ndan x^2 terimlerini kald─▒rabiliriz ve denklemi a┼¤a─¤─▒daki forma sokar─▒z

Bu denklemde k'n─▒n yan─▒na c^2 (c: ─▒┼¤─▒k h─▒z─▒) koyarsak k sabitimiz birimsiz bir say─▒sal de─¤ere d├Čn├╝┼¤├╝r.

Bu denkleme Friedman Denklemi denir. Friedman denklemi eksikleri olsa da kozmolojinin temel denklemi kabul edilir. Bu denklemdeki k sabitine ise e─¤rilik fakt├Čr├╝ (curvature factor) denir. K sabitinin pozitif, negatif ya da s─▒f─▒r olmas─▒ uzay─▒n farkl─▒ e─¤rili─¤e (forma) sahip olmas─▒ anlam─▒na gelir.
K>0 ise kapal─▒ form k├╝resel uzay, K<0 ise a├¦─▒k form hiperboloit uzay, K=0 ise a├¦─▒k form d├╝z uzay (bildi─¤imiz Euclid uzay─▒) s├Čz konusudur.

Uzay─▒n hangi formda oldu─¤unu bilmemekle beraber, Euclid uzay─▒nda oldu─¤umuzu d├╝┼¤├╝n├╝yoruz. Bu konudaki ├Čl├¦├╝mler (high precision cosmology) geli┼¤irse ileride belki bizi ┼¤a┼¤─▒rtacak bir sonu├¦la da kar┼¤─▒la┼¤abiliriz. K>0 ise (uzay kapal─▒ k├╝resel formda ise) bu ┼¤u anlama gelir:
T─▒pk─▒ bir k├╝renin y├╝zeyinde (├Črne─¤in d├╝nyam─▒zda) s├╝rekli ayn─▒ y├Čne ilerledi─¤imizde nas─▒l bir s├╝re sonra ba┼¤lad─▒─¤─▒m─▒z noktaya geri d├Čn├╝yorsak k├╝resel uzayda da ayn─▒ ┼¤ey s├Čz konusu olur. Bu sefer bir y├╝zey ├╝zerinde de─¤il de 3 boyutlu uzayda ilerlemi┼¤ oluruz, tek fark budur. Ben e─¤rilik fakt├Čr├╝n├╝n s─▒f─▒rdan b├╝y├╝k olmas─▒n─▒ daha heyecanl─▒ buluyorum (umar─▒m bir g├╝n b├Čyle oldu─¤u ortaya ├¦─▒kar..)
Friedman Denklemini elde etti─¤imize g├Čre bu denklemde yer alan, zamana g├Čre de─¤i┼¤en ba─¤─▒ml─▒ de─¤i┼¤keni (├Čl├¦ek fakt├Čr├╝n├╝) d├╝z uzay (k=0) kabul├╝yle elde etmeye ├¦al─▒┼¤al─▒m. ├¢l├¦ek fakt├Čr├╝ bize uzay─▒n zamana g├Čre nas─▒l geni┼¤ledi─¤ini (ya da darald─▒─¤─▒n─▒) g├Čsteren ve Hubble Parametresinde yer alan ├Čnemli bir de─¤i┼¤kendir. Friedman denklemi do─¤rusal olmayan bir diferansiyel denklemdir ve analitik ├¦├Čz├╝m├╝ ├¦ok kolay de─¤ildir. Bu t├╝r denklemlerin ├¦├Čz├╝m├╝nde s─▒k├¦a ba┼¤vurulan bir y├Čntem tahmini bir de─¤er ile ├¦├Čz├╝m├╝ sorgulamakt─▒r. ├¢l├¦ek fakt├Čr├╝ zamana ba─¤l─▒ bir fonksiyondur ve polinom formunda olabilece─¤i gibi ├╝stel ya da logaritmik vb. formda da olabilir. Friedman denkleminde e┼¤itli─¤in sa─¤ taraf─▒ s─▒f─▒rdan farkl─▒ bir de─¤er oldu─¤undan e┼¤itli─¤in sol taraf─▒ asla bir b├╝k├╝m noktas─▒na sahip olmamal─▒d─▒r (a de─¤i┼¤keni zamanla s├╝rekli artan ya da s├╝rekli azalan bir de─¤i┼¤ken olmal─▒d─▒r). Uzay s├╝rekli daralamayaca─¤─▒na g├Čre s├╝rekli geni┼¤lemelidir, buradan bu sonu├¦ ├¦─▒k─▒yor. O halde a zamanla artan pozitif bir de─¤erdir. a=c.t^p diyelim.

Sonucu III nolu denklemde (k=0) yerine yazarsak ├¦├Čz├╝m├╝ a┼¤a─¤─▒daki ┼¤ekilde elde etmi┼¤ oluruz.


a i├¦in elde etti─¤imiz yukar─▒daki VI numaral─▒ denklem bize uzay─▒n zamana g├Čre ne ┼¤ekilde geni┼¤ledi─¤ini g├Čsteriyor.
Rahmetli bu denklemi (III nolu denklem) Einstein'─▒n genel g├Črelilik kuram─▒ndan t├╝retmi┼¤tir, ancak bu denklem Newton mekani─¤inden de t├╝retilebiliyor. Buradaki ├¦├Čz├╝mlemedeki enerji yo─¤unlu─¤u olarak k├╝tle esas al─▒nm─▒┼¤t─▒r (mass dominated universe kabul├╝ yap─▒lm─▒┼¤t─▒r). Ancak uzay ilk zamanlarda ├¦ok daha dard─▒ ve fotonlar─▒n dalga boylar─▒ k├╝├¦├╝k dolay─▒s─▒yla frekanslar─▒ ve enerji d├╝zeyleri y├╝ksekti. Uzay─▒n bu ilk zamanlar─▒ i├¦in enerji yo─¤unlu─¤u olarak fotonlar─▒ esas alan (radiation dominated universe) bir ├¦├Čz├╝mleme de yap─▒labilir. Bu ├¦├Čz├╝mleme yap─▒l─▒rsa uzay─▒n ilk zamanlar t'nin 2/3 de─¤il de 1/2 kuvveti oran─▒nda geni┼¤ledi─¤i ortaya ├¦─▒k─▒yor. Bu ├¦├Čz├╝mlemeyi dahil etmedim, gerek de yok, olan olmu┼¤ bir kere.. ┼×imdi k├╝tle esasl─▒ ├¦├Čz├╝m yapmal─▒, biz de onu yapt─▒k zaten..
"Evrende en b├╝y├╝k ziyan, sorgulama yetene─¤ini yitirmi┼¤ bir beyindir." - A. Einstein
-

asymptote - Mesajlar: 12140
- Kay─▒t: 11 Ara 2010, 14:28
D├Čn TSF Sohbet - Off Topic Discussion
Kimler ├¦evrimi├¦i
Bu forumu gezen kullan─▒c─▒lar: Hi├¦ bir kay─▒tl─▒ kullan─▒c─▒ yok ve 4 misafir
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Advertisements by Advertisement Management
|
||||||||||||||
All brand names and trademarks are the property of their respective owners